How To Do Regression Analysis On Multiple Sets Of Data In Excel For Mac

On the “Add-Ins” button and select the “Analysis ToolPak” and click the “Go” button to install. Kindle for mac 64 bit. The “Data Analysis” tab should then appear in the “Data” menu as shown above To run the regression, arrange your data in columns as seen below. Click on the “Data” menu, and then choose the “Data Analysis” tab. Office 2016 for mac ppt to mp4 audio workout. Multiple Regression Analysis with Excel Zhiping Yan November 24, 2016 1849 1 comment Simple regression analysis is commonly used to estimate the relationship between two variables, for example, the relationship between crop yields and rainfalls or the relationship between the taste of bread and oven temperature.

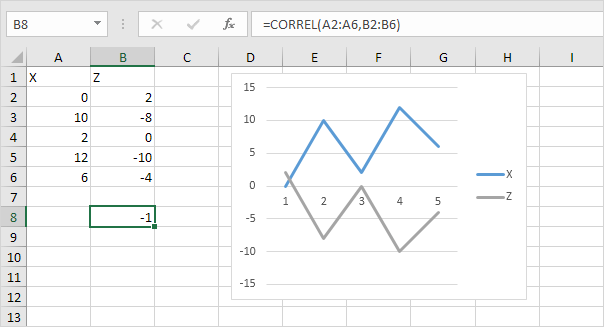
By Excel’s regression functions let you perform regression analysis. In a nutshell, regression analysis involves plotting pairs of independent and dependent variables in an XY chart and then finding a linear or exponential equation that describes the plotted data.

FORECAST: Forecast dependent variables using a best-fit line The FORECAST function finds the y-value of a point on a best-fit line produced by a set of x- and y-values given the x-value. The function uses the syntax =FORECAST(x,known_y's,known_x's) where x is the independent variable value, known_y’s is the worksheet range holding the dependent variables, and known_x’s is the worksheet range holding the independent variables.

The FORECAST function uses the known_y’s and known_x’s values that you supply as arguments to calculate the y=mx+b equation that describes the best-fit straight line for the data. The function then solves that equation using the x argument that you supply to the function. To use the linear regression functions such as the FORECAST function, remember the equation for a line is y=mx+b. Y is the dependent variable, b is the y-intercept or constant, m is the slope, and x gives the value of the independent variable. INTERCEPT: y-axis intercept of a line The INTERCEPT function finds the point where the best-fit line produced by a set of x- and y-values intersects the y-axis. The function uses the syntax =INTERCEPT(known_y's,known_x's) where known_y’s is the worksheet range holding the dependent variables and known_x’s is the worksheet range holding the independent variables.

If you’ve ever plotted pairs of data points on an XY graph, the way the INTERCEPT function works is pretty familiar. The INTERCEPT function uses the known_y’s and known_x’s values that you supply as arguments to calculate the best-fit straight line for the data — essentially figuring out the y=mx+b equation for the line. The function then returns the b value because that’s the value of the equation when the independent, or x, variable equals zero. LINEST The LINEST function finds the m and b values for a line based on sets of and variables.

The function uses the syntax =LINEST(known_y's,[known_x's],[const],[stats]) where known_y’s equals the array of y-values that you already know, known_x’s supplies the array of x-values that you may already know, const is a switch set to either TRUE (which means the constant b equals 0) or to FALSE (which means the constant b is calculated), and is another switch set to either TRUE (meaning the function returns a bunch of other regression statistics) or FALSE (meaning enough already). SLOPE: Slope of a regression line The SLOPE function calculates the slope of a regression line using the x- and y-values. The function uses the syntax =SLOPE(known_y's,known_x's) An upward slope indicates that the independent, or x, variable positively affects the dependent, or y, variable. In other words, an increase in x produces an increase in y. A downward slope indicates that the independent, or x, variable negatively affects the dependent, or y, variable. The steeper the slope, the greater the effect of the independent variable on the dependent variable.